Numerical Integrations

The Trapezoid Rule:

The integral of function f(x) is the area under the curve of the function y=f(x) between two x values.

The area under the curve can be divided into a number of strips; the area of each strip is approximated as a trapezoid.

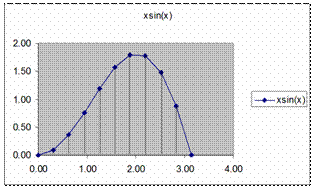
For example, to evaluate the integral: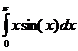

If the area under the curve is divided into N strips,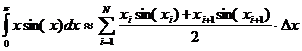

where, is the width of a strip for x between 0 and π; and there are N+1 data points, the ith point, and y_i = x_isin(x_i).

FORTRAN code for this summation is:

sum = 0

DO i = 1, N

sum = sum + (((i-1)*dx*sin((i-1)*dx)+i*dx*sin(i*dx))/2)*dx

END DO

or a bit more clearly:

! Use two arrays for x and y values, x(i) and y(i), i=1,N+1

DO i = 1, N+1

x(i) = (i-1) * dx

y(i) = x(i)*sin(x(i))

END DO

! integration

sum = 0

DO i = 1, N

sum = sum + ((y(i)+y(i+1))/2)*dx

END DO

The Simpson one-third rule:

The integration I is approximately equal to

The number of strips, N must be an even number. There are N+1 data points, the ith point x_i and y_i can be calculated same as before. The integration can be computed using a DO loop with an increment step of 2.

sum = 0

DO i = 1, N-1, 2

sum = sum + (y(i)+4*y(i+1)+y(i+2))*dx

END DO

sum = sum/3

Exercise

Write a FORTRAN program to evaluate the integral 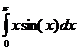. The exact integration is π. Compare the errors of the two approximations using the trapezoid rule and the Simpson one-third rule.