Next:
(ix) Lattice statistical models
Up:Quantum field theory
Previous:(vii) Boundaries
and impurities
Due to the general motivation of the entire area, many of the aforementioned
results are of a rather formal mathematical nature and very often lack
a direct link to physical application. Nonetheless, lately the experimental
techniques have advanced to such an extent that one can realistically
hope to be able to use the entire arsenal of non-perturbative techniques
for the computation of physical quantities which are directly accessible
to experiments. We can imagine that our IQFT describes a one dimensional
quantum wire, possibly finite such that the boundaries capture the effects
from the constrictions or with some impurities. Then one quantity which
can be measured very easy without disturbing the system too much is the conductance
(conductivity). In [26
,27
] we considered impurity systems and addressed the question to which
extend one can use the above mentioned techniques to compute the conductance
in the framework of a Landauer semi-classical transport theory [
98
] or the Kubo formula [97
] which is the outcome of a dynamical linear-response theory. In the
first description one requires the density distributions which are accessible
through a TBA analysis (see (iii)) and in the second, the key quantity
needed is the current-current correlation function which can be computed
along the lines described above. We adopted the techniques to this set up
and could demonstrate that both methods lead to the same results. In [
25
] we compared the conductance of a quantum wire described by a theory
which included unstable particles with the one obtained from a double defect
system and showed that they are qualitatively the same. Surprisingly, when
computing the conductance of a quantum wire described by ATFT [
30
], we obtained in some cases rational values for the filling fractions
which resemble those of the famous Jain [90
] sequence occurring in the context of the quantum Hall effect. The
other application we studied was concerned with the question whether it
is possible to generate harmonic spectra when a three dimensional laser
field is coupled to a one dimensional quantum wire [
32
]. High harmonic generation is the non-linear response of a medium (a
crystal, an atom, a gas, ...) to a laser field. The importance of harmonic
generation is related to the fact that it allows to convert infrared input
radiation of frequency 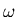 into light in the extreme ultraviolet regime whose frequencies are multiples
of
into light in the extreme ultraviolet regime whose frequencies are multiples
of 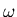 (nowadays even up to the order
(nowadays even up to the order 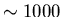 ). In gases, composed of atoms or small molecules, this phenomenon is
well understood. In more complex systems, however, for instance solid state
materials, or larger molecules, high-harmonic generation is still an open
problem. This is due to the fact that, until a few years ago, such systems
were expected not to survive the strong laser fields one needs to produce
such effects. However, nowadays, with the advent of ultrashort pulses,
there exist solid-state materials whose damage threshold is beyond the
required intensities of
). In gases, composed of atoms or small molecules, this phenomenon is
well understood. In more complex systems, however, for instance solid state
materials, or larger molecules, high-harmonic generation is still an open
problem. This is due to the fact that, until a few years ago, such systems
were expected not to survive the strong laser fields one needs to produce
such effects. However, nowadays, with the advent of ultrashort pulses,
there exist solid-state materials whose damage threshold is beyond the
required intensities of 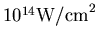 [100
]. As a direct consequence, there is an increasing interest in such materials
as potential sources for high-harmonics. In fact, several groups are currently
investigating this phenomenon in systems such as thin crystals [
1
,87
], carbon nanotubes [2
], or organic molecules [91
,4
]. Therefore our prediction [32
] that high harmonics can be generated from solid state material is very
important. Here one still has to explore a huge territory, as essentially
all measurable quantities can be expressed in some way in terms of correlation
functions. With regard to the conductance there is of course the need
to consider more types of models, refine the techniques and especially
important is to include temperature on the side of the Kubo formula description.
Concerning the filling fractions the interesting question of a possible
deeper relation to the fractional quantum Hall effect needs to be answered.
[100
]. As a direct consequence, there is an increasing interest in such materials
as potential sources for high-harmonics. In fact, several groups are currently
investigating this phenomenon in systems such as thin crystals [
1
,87
], carbon nanotubes [2
], or organic molecules [91
,4
]. Therefore our prediction [32
] that high harmonics can be generated from solid state material is very
important. Here one still has to explore a huge territory, as essentially
all measurable quantities can be expressed in some way in terms of correlation
functions. With regard to the conductance there is of course the need
to consider more types of models, refine the techniques and especially
important is to include temperature on the side of the Kubo formula description.
Concerning the filling fractions the interesting question of a possible
deeper relation to the fractional quantum Hall effect needs to be answered.
Next:
(ix) Lattice statistical models
Up:Quantum field theory
Previous:(vii) Boundaries
and impurities