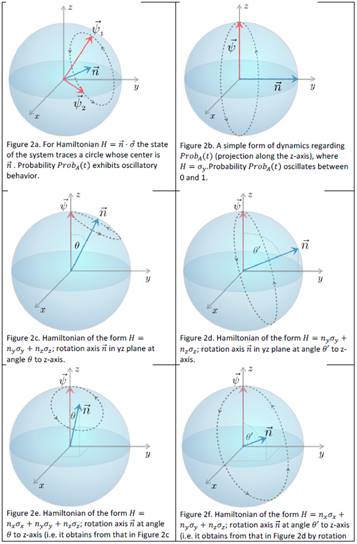
Welcome to the page of
Marie Curie project H2020-MSCA-IF-2015 grant 696331, awarded to Dr. Irina
Basieva and Dr. Emmanuel Pothos, at City, University of London.
This project explores the potential
of quantum theory to provide formal models for belief updating and rumination/
ambivalence in cognition. Quantum theory is used as a basis for a cognitive
model, and no assumptions are made about the brain (we assume a classical
brain). The slides from a recent talk summarizing the quantum cognition
programme can be found here.
|
|
|
|
This project concerns two
themes:
1) What are the principles that guide belief updating,
especially under circumstances when the decision maker receives surprising
information.
2) The structure of ambivalence or rumination,
when decision makers are faced with complex problems.
Navigate down to the
following sections:
*collaborators
We summarize each theme
separately:
|
Belief updating.
We experimentally
observed violations of classical, Bayesian updating of belief. As shown,
updating on strong evidence can lead to a dramatic increase of confidence
(from zero, practically denying the possibility) to almost complete
confidence. We explained how and why quantum probability theory can be
applied to describe the experimental results and resolved the zero-prior
trap, in a way which is more efficient than following Cromwell’s rule
(applying only non-zero and non-one probabilities to all the options). This
work provides new insights potentially applicable in the experimental and
theoretical study of the phenomenon of creativity, which can be interesting
not only for cognitive psychology but also for more applied subjects, such as
artificial intelligence (this work was primarily reported in Basieva et al.,
2017). |
Rumination/
ambivalence. For the first time we
explored ambivalence in decision making, using an innovative experimental
paradigm and data collection via eye tracking and mouse tracking. (The data
we collected from eye tracking corresponded to momentary shifts in attention
during decision making, which under some assumptions, can be associated with
propensities for different decisions.) The empirical data was modelled with a
sophisticated open system dynamics quantum model, which is characterized by
initial oscillatory behaviour (corresponding to an early period of
ambivalence) followed by stabilization (corresponding to reaching a decision,
which may still involve uncertainty). We also argued that the more common
drift diffusion models are poorly suited to describe our empirical results,
because of the multiple reversals in decision propensities. The open systems
quantum model provided excellent fits and the model parameters revealed
decision structure in the eye tracking dynamics (less so in mouse tracking
dynamics, though for reasons which may relate to the fidelity of data). |
|
Note: The belief updating
experimental investigation was based on a crime mystery with a surprising suspect!
|
Note: The experimental work in
this strand was based on eye-tracking methods.
|
Our
collaborators
Dr. M. Asano, Tokuyama
College of Technology (in relation to quantum dynamics).
Prof. F. Bagarello, University of Palermo (in relation to state
dependence in Heisenberg inequality and number operators in quantum field
theory).
Dr. A. Barque-Duran, City
University (in relation to design of MouseTracking
experiments)
Dr. J. Broekaert, Indiana
University (in relation to open system dynamics; this association started while
Dr. Broekaert was at City).
Dr. P. Blaziak,
Institute of Nuclear Physics Polish Academy of Sciences,31342 Krakow, Poland
(in relation to dynamics of quantum systems)
Dr. A. Gloeckner,
University of Hagen (in relation to drift diffusion models)
Dr. A. Khrennikov,
University of Linnaeus
Dr. A. Sholz,
University of Zurich (in relation to ambivalence in decision making and eye
tracking)
Dr. J. Trueblood,
Vanderbilt University (in relation to quantum updating).
Dr. B. von Helversen,
University of Zurich (in relation to ambivalence in decision making and eye
tracking)
Note: all publications are deposited at the City Research Online open
access depository.
Irina Basieva,
Emmanuel Pothos, Jennifer Trueblood, Andrei Khrennikov, Jerome Busemeyer,
Quantum probability updating from zero priors (by-passing Cromwell’s rule),
Journal of Mathematical Psychology 77 (2017), 58-69
Abstract:
Cromwell’s rule (also
known as the zero priors paradox) refers to the constraint of classical
probability theory that if one assigns a prior probability of 0 or 1 to a
hypothesis, then the posterior has to be 0 or 1 as well (this is a
straightforward implication of how Bayes’ rule works). Relatedly, hypotheses
with a very low prior cannot be updated to have a very high posterior without a
tremendous amount of new evidence to support them (or to make other
possibilities highly improbable). Cromwell’s rule appears at odds with our
intuition of how humans update probabilities. In this work, we report two
simple decision making experiments, which seem to be inconsistent with
Cromwell’s rule. Quantum probability theory, the rules for how to assign
probabilities from the mathematical formalism of quantum mechanics, provides an
alternative framework for probabilistic inference. An advantage of quantum
probability theory is that it is not subject to Cromwell’s rule and it can
accommodate changes from zero or very small priors to significant posteriors.
We outline a model of decision making, based on quantum theory, which can
accommodate the changes from priors to posteriors, observed in our experiments.
Highlights:
According to classical
probability, belief updating follows Bayes’s law: 
, so that the degree of belief revision depends on the
ratio of the priors 
. This means that very unlikely hypotheses (low 
) will be revised only to a limited extent, regardless
of how strong the evidence is.
According to quantum theory,
belief updating follows Luder’s law: 
, where the ‘P’ objects are projection operators in
quantum theory. Luder’s law allows jumps from priors to posteriors of any size,
even when the priors are very low.
We tested participants with a
crime mystery: participants were presented with a hypothetical theft scenario.
The initial information made some suspects more likely, others very unlikely.
Following new information, participants were asked to re-evaluate the
likelihood of different suspects being guilty. We modelled belief updating with
both probability rules and concluded that the quantum one provided better
description than the classical one.
Irina Basieva,
Polina Khrennikova, Emmanuel M. Pothos, Masanari Asano, & Andrei Khrennikov
(in press). Quantum-like model of subjective expected utility. Journal of
Mathematical Economics.
Abstract:
We present a very general
quantum-like model of lottery selection based on representation of beliefs of
an agent by pure quantum states. Subjective probabilities are mathematically
realized in the framework of quantum probability (QP). Utility functions are
borrowed from the classical decision theory. But in the model they are
represented not only by their values. Heuristically one can say that each value
ui = u(xi) is surrounded by a cloud of information
related to the event (A, xi). An agent processes this information by
using the rules of quantum
information and QP. This process is very complex; it combines counterfactual
reasoning for comparison between preferences for different outcomes of
lotteries which are in general complementary. These comparisons induce
interference type effects (constructive or destructive). The decision process
is mathematically represented by the comparison operator and the outcome of
this process is determined by the sign of the value of corresponding quadratic
form on the belief state. This operational process can be decomposed into a few
subprocesses. Each of them can be formally treated as a comparison of
subjective expected utilities and interference factors (the latter express, in
particular, risks related to lottery selection). The main aim of this paper is
to analyze the mathematical structure of these
processes in the most general situation: representation of lotteries by
noncommuting operators.
Jan Broekaert,
Irina Basieva, Pawel Blasiak, Emmanuel M. Pothos, Quantum-like dynamics applied
to cognition: a consideration of available options, Philosophical Transactions
of the Royal Society A: Mathematical, Physical and Engineering Sciences 375
(2017), 20160387
Abstract:
Quantum Probability Theory
(QPT) has provided a novel, rich mathematical framework for cognitive
modelling, especially for situations which appear paradoxical from classical
perspectives. This work concerns the dynamical aspects of QPT, as relevant to
cognitive modelling. We aspire to shed light on how the mind’s driving potentials
(encoded in Hamiltonian and Lindbladian operators)
impact the evolution of a mental state. Some existing QPT cognitive models do
employ dynamical aspects when considering how a mental state changes with time,
but it is often the case that several simplifying assumptions are introduced.
What kind of modelling flexibility do QPT dynamics offer without any
simplifying assumptions and is it likely that such flexibility will be relevant
in cognitive modelling? We consider a series of nested QPT dynamical models,
constructed with a view to accommodate results from a simple, hypothetical
experimental paradigm on decision making. We consider Hamiltonians more complex
than the ones which have traditionally been employed with a view to explore the
putative explanatory value of this additional complexity. We then proceed to
compare simple models with extensions regarding both the initial state (e.g.,
mixed state with a specific orthogonal decomposition; a general mixed state)
and the dynamics (by introducing Hamiltonians which destroy the separability of
the initial structure and by considering an open-systems extension). We
illustrate the relations between these models mathematically and numerically.
Highlights:
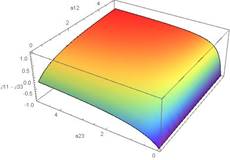
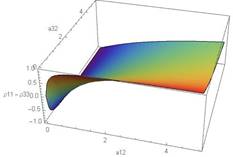
This figure provides a
helpful illustration of the dynamical options provided by various combinations
of the Pauli spin matrices.
A link to a technical
presentation outlining this work is here.
Sholz, A.,
Basieva, I., Barque-Duran, A., Gloeckner, A., von
Helversen, B, & Pothos, E. M. (in preparation). Characterizing structure in
eye tracking data.
Abstract:
Eye tracking has been
extensively employed to study momentary shifts in attention during decision
making and several researchers have attempted to establish links between
characteristics of eye tracking dynamics and more directly relevant behavioral variables (e.g., the actual decisions). However,
to our knowledge there have not been any attempts to directly model eye
tracking dynamics in a decision task, including based on the dominant framework
for decision dynamics generally, drift diffusion models. Can drift diffusion
models be employed to describe eye tracking dynamics in a decision task? We
argue that such models are not ideally suited to the task at hand and so
motivate an alternative framework, based on open systems quantum theory. We
model eye tracking curves from a decision task and explore the interpretability
of parameters.
Highlights:
We considered everyday
‘complex’ decision problems, for example the decision of whether a hypothetical
couple would decide to keep a stray dog or not, based on information about the
criteria relevant to that couple. For example, the arguments would be (arranged
in the same way as would be presented to participants):
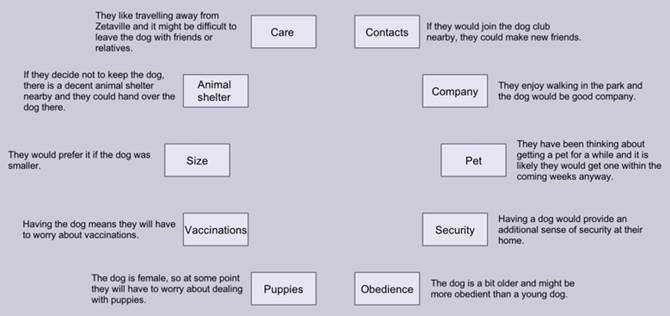
Our guiding consideration
of interest was that the resolution of these (there were three) decision
dilemmas would involve a process of back and forth – an intuition that one
decision is better followed by an intuition that the other decision is better –
for a number of cycles, before converging to the eventual decision.
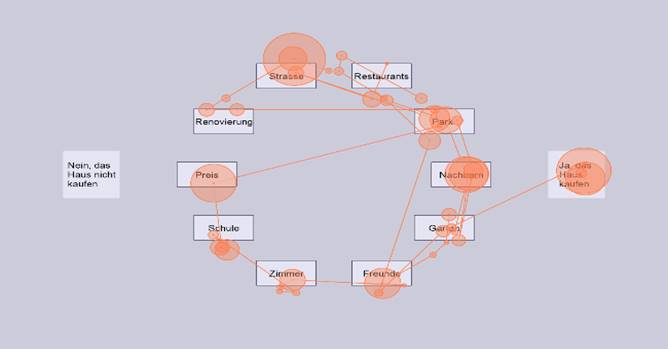
We employed eye tracking to monitor momentary
attentional shifts, which are generally thought to be related to attentional
propensities. The following figure provides a typical scanpath illustrating the
assumption that for ‘complex’ problems of this sort there are multiple
reversals in attentional focus (and, we believe, attentional propensities,
though it is important to note that this was not directly tested in this work).
For the modelling we
employed a quantum model based on open system dynamics. A prior, this is a
suitable choice, because open system dynamics in quantum theory follow a
pattern of initial oscillation (which cognitively can be associated with
initial ambivalence) giving rise to a stable pattern (which cognitively can be
associated with stabilization or resolution of opinion, which can still include
some uncertainty). We note the form of the model, without commentary:
, where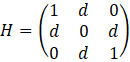 
We also present these diagrams
as illustrations of model behaviour.
|
|
|
|
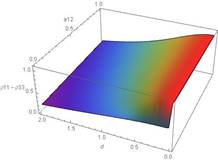
Illustrating the six parameter; in all
cases the vertical shows 
at large times. The left figure illustrates
the way dominance for yes response requires both drift for a yes response (
)
and drift away from a no response (
),
even if the former influence is more important, with other parameters set as d=0.1, 
and adjT=1 (in all cases). The middle figure shows how drift for
a yes response ()
balances out drift for a no response (
),
with other parameters as 
.
The right illustrates that high values of d
prevent strong dominance of (e.g.) yes
response; other parameters 
.
Empirical results favoured
the quantum model. A presentation outlining the key model elements can be found
here.
Fabio
Bagarello, Irina Basieva, Emmanuel M. Pothos, Andrei Khrennikov, Quantum like modeling of decision making: Quantifying uncertainty with
the aid of Heisenberg–Robertson inequality, Journal of Mathematical Psychology
84 (2018) 49-56
Abstract:
This paper contributes to
quantum-like modeling of decision making (DM) under
uncertainty through application of Heisenberg's uncertainty principle (in the
form of the Robertson inequality). In this paper we apply this instrument to
quantify uncertainty in DM performed by quantum-like agents. As an example, we
apply the Heisenberg uncertainty principle to the determination of mutual
interrelation of uncertainties for “incompatible questions” used to be asked in
political opinion pools. We also consider the problem of representation of
decision problems, e.g., in the form of questions, by Hermitian operators,
commuting and noncommuting, corresponding to compatible and incompatible
questions respectively. Our construction unifies the two different situations
(compatible versus incompatible mental observables), by means of a single
Hilbert space and of a deformation parameter which can be tuned to describe
these opposite cases. One of the main foundational consequences of this paper
for cognitive psychology is formalization of the mutual uncertainty about
incompatible questions with the aid of Heisenberg's uncertainty principle
implying the mental state dependence of (in)compatibility of questions.
Fabio Bagarello,
Irina Basieva, Andrei Khrennikov, Quantum field inspired model of decision
making: Asymptotic stabilization of belief state via interaction with
surrounding mental environment, Journal of Mathematical Psychology 82 (2018)
159 – 168
Irina Basieva,
Andrei Khrennikov, Decision-Making and Cognition Modeling
from the Theory of Mental Instruments, Chapter in a book The Palgrave Handbook
of Quantum Models in Social Science (2017), pp 75-93.
Masanari
Asano, Irina Basieva, Emmanuel Pothos, Andrei Khrennikov, State Entropy and
Differentiation Phenomenon, Entropy 20/6 (2018), 394.
Abstract:
In the formalism of
quantum theory, a state of a system is represented by a density operator.
Mathematically, a density operator can be decomposed into a weighted sum of
(projection) operators representing an ensemble of pure states (a state
distribution), but such decomposition is not unique. Various pure states
distributions are mathematically described by the same density operator. These
distributions are
categorized into classical ones obtained from the Schatten
decomposition and other, non-classical, ones. In this paper, we define the
quantity called the state entropy. It can be considered as a generalization of
the von Neumann entropy evaluating the diversity of states constituting a
distribution. Further, we apply the state entropy to the analysis of
non-classical states created at the intermediate stages in the process of
quantum measurement. To do this, we employ the model of differentiation, where
a system experiences step by step state transitions under the influence of
environmental factors. This approach can be used for modeling
various natural and mental phenomena: cell’s differentiation, evolution of
biological populations, and decision making.
Emmanuel M. Pothos,
Irina Basieva, Albert Barque-Duran, Katy Tapper, Andrei Khrennikov, Information
overflow and persistent disagreement (in preparation)
Abstract:
There have been concerns
that modern political debate involves less truth and more truthiness. A key aspect
of truthiness is persistent disagreement. We focus on factual questions (i.e.,
ones not depending on personal preference or values) and for well-meaning
individuals (who try to mitigate the influence of careless processing,
emotions, or other biases). We recognize information overflow as an important
characteristic of modern political debate. Heuristics and biases research
provides several insights for why individuals may disagree, but less if they
are well-meaning. Classical probability theory (CPT) can explain why reasoners
would be challenged under circumstances of information overflow, because of the
requirement of constructing large Boolean algebras: it makes sense to break a
complex question, e.g. Brexit, into smaller themes, however, CPT does not provide
a prescription for doing so. Quantum probability theory (QPT), the rules for
probabilistic assignment from quantum mechanics, formalizes the way a Boolean
algebra can be simplified into a partial Boolean algebra, through the QPT
notion of incompatibility (incompatible questions cannot have a joint
probability distribution). The price for this simplification is a picture of
the world which may be inaccurate. We discuss further implications and possible
ameliorating procedures for reducing this kind of truthiness in modern
political debate.
Andrei
Khrennikov, Irina Basieva, Emmanuel M. Pothos, & I. Yamato (in press).
Quantum probability in decision making from quantum information representation
of neuronal states. Scientific Reports.
Abstract:
The recent wave of
interest to modeling the process of decision making
with the aid of the quantum formalism gives rise to the following question:
‘How can neurons generate quantum-like statistical data?’ (There is a plenty of
such data in cognitive psychology and social science.) Our model is based on
quantum-like representation of uncertainty in generation of action potentials.
This uncertainty is a consequence of complexity of electrochemical processes in
the brain; in particular, uncertainty of triggering an action potential by the
membrane potential. Quantum information state spaces can be considered as
extensions of classical information spaces corresponding to neural codes; e.g.,
0/1, quiescent/firing neural code. The key point is that processing of information
by the brain involves superpositions of such states. Another key point is that
a neuronal group performing some psychological function F is an open quantum
system. It interacts with the surrounding electrochemical environment. The
process of decision making is described as decoherence in the basis of
eigenstates of F: A decision state is a steady state. This is a linear
representation of complex nonlinear dynamics of electrochemical states.
Linearity guarantees exponentially fast convergence to the decision state.
The research carried out
concerns belief updating and rumination/ ambivalence. Belief updating is about
how we update our beliefs, in light of presented information. A simple example is
this: suppose you are interested in whether it is likely to rain or not (this
is your belief). It is autumn and you have some expectations of whether it is
likely to rain or not. But then you look out of the window and receive some
information, say it is really sunny. How does this new information change your
belief? Rumination/ ambivalence concerns how we deal with complex decisions. By
complex decisions, we mean decisions such that the best option is just not
(perhaps immediately) obvious. Consider the issue of trying to get a jumper and
you narrow down your choice between a green and a blue one. There is no simple
‘utility’ to make you decide, since the considerations that favour either
option may be complex and not matched. We believe that such decision problems
involve a process of going back and forth, before eventually settling on a
particular decision.
We have created a brief article expanding on these ideas,
which can be found here.