Next:
(v) Identification of the
Up:Quantum field theory
Previous:Renormalization
group flow
As mentioned above, in accordance with Wightman's reconstruction theorem
[118
] the 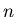 -point functions are the heart of a QFT. Once the form factors for a
particular operator have been determined one is in principle in the position
to compute the correlation functions by expanding them in terms of
-point functions are the heart of a QFT. Once the form factors for a
particular operator have been determined one is in principle in the position
to compute the correlation functions by expanding them in terms of 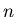 -particle form factors. Based on the study of different individual models
supplemented with some heuristics, it has turned out that this series converges
very fast. Thus, from a practical point of view, with regard to the computation
of correlation functions, it is sufficient to determine just the first
-particle form factors. Based on the study of different individual models
supplemented with some heuristics, it has turned out that this series converges
very fast. Thus, from a practical point of view, with regard to the computation
of correlation functions, it is sufficient to determine just the first 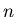 -particle form factors. We demonstrated [20
], however, that once the rank of the algebra increases, the convergence
of the series becomes worse. So far most of these computations are carried
out numerically using Monte Carlo methods and it is clear that this has
certain limitations when the convergence becomes poor. Conceptually
one still needs to establish rigorously whether the above sums converge
at all and if so under which circumstances. The main technical problems to
be solved is to carry out the infinite sum over the intermediate states.
Taking the log of the two-point function there has been a proposal [
111
] which could ease the computational task and indeed there has been some
recent progress [6
] along these lines at least for the case of the Ising and sinh-Gordon
model.
-particle form factors. We demonstrated [20
], however, that once the rank of the algebra increases, the convergence
of the series becomes worse. So far most of these computations are carried
out numerically using Monte Carlo methods and it is clear that this has
certain limitations when the convergence becomes poor. Conceptually
one still needs to establish rigorously whether the above sums converge
at all and if so under which circumstances. The main technical problems to
be solved is to carry out the infinite sum over the intermediate states.
Taking the log of the two-point function there has been a proposal [
111
] which could ease the computational task and indeed there has been some
recent progress [6
] along these lines at least for the case of the Ising and sinh-Gordon
model.
Next:
(v) Identification of the
Up:Quantum field theory
Previous:Renormalization
group flow