Next:
(vi) Organizing and extending
Up:Quantum field theory
Previous:(iv) Correlation
functions
The central concepts of relativistic QFT, like Einstein causality
and Poincaré covariance, are captured in local field equations and
commutation relations. As a matter of fact local quantum physics (algebraic
quantum field theory) [85
] takes the collection of all operators localized in a particular region,
which generate a von Neumann algebra, as its very starting point. On the
other hand, as we outlined above in the formulation of a QFT one may alternatively
start from a particle picture and investigate the corresponding scattering
theories. Ignoring subtleties of non-asymptotic states, it is essentially
possible to obtain the latter picture from the former by means of the LSZ-reduction
formalism [99
]. However, the question of how to reconstruct at least part of the field
content from the scattering theory is in general still an outstanding issue.
In the context of 1+1 dimensional IQFTs the identification of the operators
is based on the assumption, dating back to the initial papers [
117
], that each solution to the form factor consistency equations corresponds
to a particular local operator. Based on this, numerous authors have used
various ways to identify and constrain the specific nature of the operator,
e.g. by looking at asymptotic behaviours, performing perturbation theory,
taking symmetries into account, formulating quantum equations of motion,
etc. We carried out an analysis [20
] for the SU(3)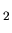 -HSG model identifying each of our many solutions with a local operator
and matching it with a counterpart in the ultraviolet conformal field theory,
hence organizing and identifying the operator content. An additional
organizing principle comes from the cluster properties. In space they are
quite familiar and intuitive, corresponding to the observation that far separated
operators do not interact. In 1+1 dimensions a similar property has also
been noted in momentum space. It states that whenever the first, say
-HSG model identifying each of our many solutions with a local operator
and matching it with a counterpart in the ultraviolet conformal field theory,
hence organizing and identifying the operator content. An additional
organizing principle comes from the cluster properties. In space they are
quite familiar and intuitive, corresponding to the observation that far separated
operators do not interact. In 1+1 dimensions a similar property has also
been noted in momentum space. It states that whenever the first, say 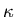 , rapidities of an
, rapidities of an 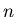 -particle form factor are shifted to infinity, the
-particle form factor are shifted to infinity, the 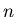 -particle form factor factorizes into a
-particle form factor factorizes into a 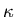 and an (
and an (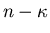 )-particle form factor which are possibly related to different types
of operators. This means the cluster property can be used as an organizing
principle amongst different types of operators and also to construct new
solutions. These properties have been analyzed explicitly for several specific
models [20
]. In general, the problem of how to reconstruct the field content
from the scattering theory is unresolved. As not many models exist for which
the above mentioned analysis has been carried out, one certainly needs
first of all more examples. At present the identification and naming of
the operators in this context is carried out with regard to the corresponding
conformal dimension in the UV-limit. Possibly one needs also to find different
types of identification criteria or quantities as it is not guaranteed that
there is a one-to-one correspondence between the operators in the massive
model and those in the corresponding conformal field theory. Conceptually
this is not clear yet and identical to the question whether so-called ``
shadow operators" [113
] exist or not.
)-particle form factor which are possibly related to different types
of operators. This means the cluster property can be used as an organizing
principle amongst different types of operators and also to construct new
solutions. These properties have been analyzed explicitly for several specific
models [20
]. In general, the problem of how to reconstruct the field content
from the scattering theory is unresolved. As not many models exist for which
the above mentioned analysis has been carried out, one certainly needs
first of all more examples. At present the identification and naming of
the operators in this context is carried out with regard to the corresponding
conformal dimension in the UV-limit. Possibly one needs also to find different
types of identification criteria or quantities as it is not guaranteed that
there is a one-to-one correspondence between the operators in the massive
model and those in the corresponding conformal field theory. Conceptually
this is not clear yet and identical to the question whether so-called ``
shadow operators" [113
] exist or not.
Next:
(vi) Organizing and extending
Up:Quantum field theory
Previous:(iv) Correlation
functions