(vi) Organizing and extending the zoo of models

Numerous studies in this subject consist of investigating some individual models. However, with regard to the general motivation one should ultimately try to extract some generic features from these studies in order to formulate some more model independent results. There are various physical or mathematical concepts one may think off to structure and classify the known solutions. For instance one might employ symmetries (quantum group, Lie group or discrete symmetries) as an organizing principle. This is quite useful, but not enough to capture all possibilities. Lie algebraic structures equip one automatically with some classification scheme and one can seek for them inside various quantities, such as the masses [76 ], the three point coupling [76 ], the higher couplings [60 ], the scattering matrix [80 ,73 ], the decoupling of unstable particles from the spectrum [ 19 ,29 ], etc. It appears that all known models can be related in some way to ATFT and based on that viewpoint I will give a brief overview of the different types of physical behaviours of these models. This is also summarized in figures 2 and 3 with my contributions indicated. Soon after the seminal paper of A. Zamolodchikov [123 ] fourteen years ago on the perturbation of the Ising model, it was realized [46 ], that most of the massive theories obtained this way are closely related to ATFTs, either in a `` minimal'' sense or with the coupling constant included. The scattering matrices of ATFT are different in physical nature depending on whether the coupling constant is real or purely complex. In the former case backscattering is absent and the Yang-Baxter equations are trivially satisfied. On the base of case-by-case studies for various algebras several explicit scattering matrices were constructed thereafter for ATFTs with real coupling [3 ]. For the simply laced algebras (ADE) this series of investigations culminated with the formulation of universal formulae which encompass all these algebras at once [80 ]. The universal nature of these representations for the scattering matrices allowed also to establish the equivalence between the bootstrap equations and a classical fusing rule formulated in terms of orbits generated by Coxeter elements of the related Lie algebra [ 76 ]. Furthermore, the fusing rule is closely linked to the quantum conservation laws. The origin for the structural interrelation between the classical and the quantum field theory is the fortunate coincidence, that for the simply laced theories all masses of the theory renormalize with an overall factor. It is the breakdown of this property for theories related to a non-simply laced algebra which constituted the main obstacle in the construction of consistent scattering matrices on the base of the bootstrap principle. In order to tackle this problem, once again numerous candidates were proposed on the base of case-by-case studies [69 ,39 ], but it remained a challenge to find a closed universal representation similar to the simply laced case for these theories, until fairly recently [73 ]. The main conceptual breakthrough towards this goal was the proposal to regard these theories in a dual sense, mathematically in a Lie algebraic way and physically equivalent to this in the strong-weak duality sense in the coupling constant and in addition the generalization of the bootstrap principle. The dual formulation of affine Toda field theories constitute some concrete simple examples for the Montonen-Olive duality [ 105 ]. For theories with purely imaginary coupling constant, the sine-Gordon (SU(2)-ATFT) is the simplest and best known. Meanwhile the S-matrices for several other algebras have also been constructed [ 106 ]. In this case one exploits the fact that the Yang-Baxter equations can be solved with the help of the representation theory of quantum groups (e.g. [93 ]). Scattering matrices related to non-abelian ATFT, namely for the specific example of the homogeneous sine-Gordon models have also been found recently [104 ]. The proposed scattering matrices consist partially of rank g copies of minimal 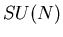$SU(N)$ -ATFT, whose mass scales are free parameters. The scattering between solitons belonging to different copies is described by an S-matrix which violates parity. These matrices possess resonance poles and the related resonance parameters which characterize the formation of unstable bound states are up to free choice. In a renormalization group analysis these resonances may be tracked down in the ``staircase patterns `` of the scaling function indicating their energy scale, which have been observed previously for similar models obtained by analytic continuation of the coupling constant [ 125 ,102 ]. However, in comparison with the models studied so far, the HSG models are distinguished in two aspects. First they break parity invariance and second the resonance poles can be associated directly to unstable particles via a classical Lagrangian. We have generalized these scattering matrices in a Lie algebraic sense [70 ]. Furthermore, we demonstrated [22 ] that it is possible to successfully implement an infinite number of resonances such that the resulting scattering matrices consist partly of elliptic functions. In [29 ] we went further and constructed new models, whose scattering matrices are made up entirely of elliptic functions and infinite products of q-deformed gamma functions.
    The open issues here are of course to complete the gaps and possibly to find models with new physical features.