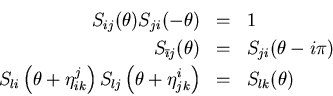(i) Scattering theory

From the above schematic diagram it is clear that the S-matrix (for the above mentioned reason I always mean by this from now on the two-particle scattering amplitude) plays a pivotal role in the bootstrap program as essentially all subsequent steps require its explicit form. By definition S is the mathematical object which relates asymptotic in-states of a theory to out-states and due to the factorization of the multi-particle S-matrix, it is possible in 1+1 dimensional IQFT to construct exact scattering matrices without any use of perturbation theory in the coupling constant or the mass. The main idea of this approach, which traces back to the middle of the seventies [112 ], is to exploit certain general physical properties of the S-matrix and set up an axiomatic system for them. One assumes that the S-matrix is unitarity, crossing invariant, consistent with the bound state bootstrap

$$\begin{eqnarray*} S_{ij}(\theta )S_{ji}(-\theta ) &=&1 \\ S_{\bar{\imath}j}(\... ... S_{lj}\left( \theta +\eta _{jk}^{i}\right) &=&S_{lk}(\theta ) \end{eqnarray*}$$

and because of integrability, that is only factorizability in the QFT, fulfills also the Yang-Baxter equations

$$S(\theta _{12})\otimes S(\theta _{13})\otimes S(\theta _{23... ...theta _{23})\otimes S(\theta _{13})\otimes S(\theta _{12}) .$$

Usually one also adds to this the concept of maximal analyticity, meaning that the S-matrix is meromorphic in the physical strip and all poles can be given a physical interpretation. It has turned out that this axiomatic system is so restrictive that it allows to determine the scattering matrices up to so-called CDD-factors [ 15 ]. There are various possible starting points to solve this set of equations: a) one may start with a specific particle spectrum (predicted for instance by a classical Lagrangian), b) one may start ad hoc with a given mass spectrum or fusing structure, c) one can start from a solution to the Yang-Baxter equation, possibly in form of a quantum group representation (see (ix)), etc. So far essentially all solutions to the set of equations could be associated with a meaningful QFT, albeit not always with a classical Lagrangian [ 70 ,22 ,29 ]. They can be characterized according to various different kinds of physical or mathematical principles (see (vi)). The two main categories the theories fall into are those in which the backscattering is absent and those which allow for it. In the first case the Yang-Baxter equations are trivially satisfied. Recently, we have extended the bootstrap principle also to models which admit unstable particles in their spectrum [ 16 ]. This required different conceptual considerations since unstable particles by their very nature can not be present in asymptotic states as they have never existed or have certainly decayed in the infinite past or future, respectively. From a purely conceptual and technical point of view it is fairly well understood how to solve the aforementioned axiomatic system of equations, at least when all particles are stable and the spectrum is finite. Nonetheless, these equations still contain various structures which can be excavated. Instead of using the usual Fourier expansion approach to solve the functional equations, we found in [ 29 ] a way to solve the functional equations by utilizing the affine Weyl group.