Next:
(iii) Consistency checks
Up:Quantum field theory
Previous:(i) Scattering theory
Wightman's reconstruction theorem [118
] states essentially that a QFT is regarded as solved once all n-point
functions are known. The n-point functions on the other hand can be expanded
in terms of form factors, which are matrix elements of local operators
between the vacuum and an 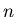 -particle state.
-particle state.
Thus the determination of form factors is an intermediate step towards
a construction of correlation functions, and therefore the entire QFT.
This idea of a form factor approach to 1+1 dimensional integrable quantum
field theories was initiated in the late seventies by Karowski and Weisz
[ 117
] and then carried forward for a long period mainly by Smirnov [
110
] until it received some wider attention about fourteen years ago [
121
]. The main strategy is similar to the above mentioned procedure of computing
the scattering matrices, that is setting up an axiomatic system (for proofs
see e.g. [5
]) for the n-particle form factors, in the hope that this system of equations
is so restrictive that it allows for their explicit computation. Remarkably,
it has turned out that this method indeed works and that the equations are
knitted in such a way that they lead to meaningful solutions. The ambiguities
in the solutions may be related to different types of operators. Based on
my contributions to the subject, I will now provide a brief account of
the state of the art on the technical status. To solve the set of consistency
equations at least for the lowest n-particle form factors is a relatively
well established general procedure, which consists of the following principle
steps: Taking the scattering matrix as an input one may anticipate the pole
structure of the n-particle form factors, independently of the nature of
the operator 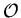 , and extract it explicitly in form of a factorizing ansatz. This might
turn out to be a relatively involved matter due to the occurrence of higher
order poles in the scattering matrix of some IQFT, but nonetheless it is
always possible. Thereafter the task of finding solutions may be reduced
to the evaluation of the so-called minimal form factors and to the problem
of solving a (usually two if bound states may be formed in the theory) recursive
equation for a polynomial which results from substituting the mentioned
ansatz into the `` form factor residue equations" which are part of the
axioms. The first task of finding the minimal form factors can be carried
out relatively easy as it only involves to solve simultaneously two functional
equations, the so-called Watson's equations. The second task is rather more
complicated and the heart of the whole problem in this approach. Having
a seed for the recursive equations, that is the lowest non-vanishing form
factor one can in general compute from them several form factors which involve
more particles. This seed could be either a known form factor when the model
reduces to some solved case or possibly the vacuum expectation value of
the operator
, and extract it explicitly in form of a factorizing ansatz. This might
turn out to be a relatively involved matter due to the occurrence of higher
order poles in the scattering matrix of some IQFT, but nonetheless it is
always possible. Thereafter the task of finding solutions may be reduced
to the evaluation of the so-called minimal form factors and to the problem
of solving a (usually two if bound states may be formed in the theory) recursive
equation for a polynomial which results from substituting the mentioned
ansatz into the `` form factor residue equations" which are part of the
axioms. The first task of finding the minimal form factors can be carried
out relatively easy as it only involves to solve simultaneously two functional
equations, the so-called Watson's equations. The second task is rather more
complicated and the heart of the whole problem in this approach. Having
a seed for the recursive equations, that is the lowest non-vanishing form
factor one can in general compute from them several form factors which involve
more particles. This seed could be either a known form factor when the model
reduces to some solved case or possibly the vacuum expectation value of
the operator 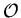 , which is not known in most cases. Unfortunately, the equations become
relatively involved after several steps. Several examples [
77
,78
,61
,17
,19
,20
,18
] have shown that often the general solution may be cast into a form
of determinants whose entries are elementary symmetric polynomials. Presuming
such a structure which, at present, may be obtained by extrapolating from
lower particle solutions to higher ones or by some inspired guess, one can
thereafter rigorously formulate proofs for such solutions. These determinant
expressions allow directly to write down equivalent integral representations,
see e.g. [17
]. There exist also different types of universal expressions like for
instance the integral representations with complicated pathes in the complex
rapidity plane presented in [110
,5
]. However, these type of expressions are sometimes only of a very formal
nature since to evaluate them concretely for higher
, which is not known in most cases. Unfortunately, the equations become
relatively involved after several steps. Several examples [
77
,78
,61
,17
,19
,20
,18
] have shown that often the general solution may be cast into a form
of determinants whose entries are elementary symmetric polynomials. Presuming
such a structure which, at present, may be obtained by extrapolating from
lower particle solutions to higher ones or by some inspired guess, one can
thereafter rigorously formulate proofs for such solutions. These determinant
expressions allow directly to write down equivalent integral representations,
see e.g. [17
]. There exist also different types of universal expressions like for
instance the integral representations with complicated pathes in the complex
rapidity plane presented in [110
,5
]. However, these type of expressions are sometimes only of a very formal
nature since to evaluate them concretely for higher 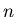 -particle form factors requires still a considerable amount of computational
effort. Besides these structures for the functional relations, for theories
which allow for backscattering, one can use the method of the nested Bethe
ansatz [5
] to capture the non-diagonal nature of some models. For the HSG models
generic expressions have been developed [17
,19
,20
,18
] already up to the general case of
-particle form factors requires still a considerable amount of computational
effort. Besides these structures for the functional relations, for theories
which allow for backscattering, one can use the method of the nested Bethe
ansatz [5
] to capture the non-diagonal nature of some models. For the HSG models
generic expressions have been developed [17
,19
,20
,18
] already up to the general case of 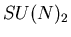 , albeit not for the entire operator content. Instead of solving the
consistency equations one may alternatively try to find representations
for particle creation operators [62
] and the local operators, using them thereafter to compute directly
the corresponding matrix elements. For the example of the Federbush model
[ 49
] we succeeded in completing this [23
] idea and compared with the outcome from the axiomatic system. We clarified
at the same time how exotic statistics (it is well known that in low dimensions
besides bosonic and fermionic statistics it is also possible to have more
generic types of statistical interactions, such as Haldane [
86
] or Gentile [83
]) can be implemented into the axiomatic system [
28
,64
] and demonstrated that these equations select out solutions which correspond
to local operators in the true sense of QFT, that is they (anti)-commute
for space-like separations. In general, it remains a challenge for
most theories to find closed analytic solutions for all
, albeit not for the entire operator content. Instead of solving the
consistency equations one may alternatively try to find representations
for particle creation operators [62
] and the local operators, using them thereafter to compute directly
the corresponding matrix elements. For the example of the Federbush model
[ 49
] we succeeded in completing this [23
] idea and compared with the outcome from the axiomatic system. We clarified
at the same time how exotic statistics (it is well known that in low dimensions
besides bosonic and fermionic statistics it is also possible to have more
generic types of statistical interactions, such as Haldane [
86
] or Gentile [83
]) can be implemented into the axiomatic system [
28
,64
] and demonstrated that these equations select out solutions which correspond
to local operators in the true sense of QFT, that is they (anti)-commute
for space-like separations. In general, it remains a challenge for
most theories to find closed analytic solutions for all 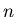 -particle form factors of a particular operator
-particle form factors of a particular operator 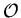 and more concrete examples are needed to be able to aim at generic
structures. Possibly they consist of building blocks made of determinants
as in [77
,78
,61
,17
,19
,20
,18
].
and more concrete examples are needed to be able to aim at generic
structures. Possibly they consist of building blocks made of determinants
as in [77
,78
,61
,17
,19
,20
,18
].
Next:
(iii) Consistency checks
Up:Quantum field theory
Previous:(i) Scattering theory