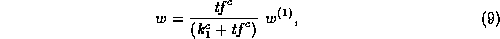Next: Document Length
Up: A Rough Model
Previous: The Shape of
What is required, therefore, is a simple 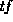 -related weight that
has something like the characteristics (a)-(d) listed in the previous
section. Such a function can be constructed as follows. The function
-related weight that
has something like the characteristics (a)-(d) listed in the previous
section. Such a function can be constructed as follows. The function
 increases from zero to an
asymptotic maximum in approximately the right fashion. The constant
determines the rate at which the increase drops off: with a large
constant, the function is approximately linear for small
increases from zero to an
asymptotic maximum in approximately the right fashion. The constant
determines the rate at which the increase drops off: with a large
constant, the function is approximately linear for small 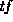 ,
whereas with a small constant, the effect of increasing
,
whereas with a small constant, the effect of increasing 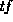 rapidly diminishes.
rapidly diminishes.
This function has an asymptotic maximum of one, so it needs to be
multiplied by an appropriate weight similar to equation 7.
Since we cannot estimate 7 directly, the obvious simple
alternative is the ordinary Robertson/Sparck Jones weight, equation
2, based on presence/absence of the term. Using the usual
estimate of 2, namely 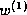 (equation 3), we obtain the
following weighting function:
(equation 3), we obtain the
following weighting function:
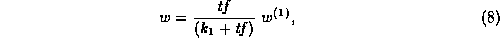
where 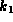 is an unknown constant.
is an unknown constant.
The model tells us nothing about what kind of value to expect for
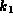 . Our approach has been to try out various values of
. Our approach has been to try out various values of 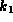 (values around 1--2 seem to be about right for the TREC data---see the
results section 7 below).
However, in the longer term we hope to use regression methods to
determine the constant. It is not, unfortunately, in a form directly
susceptible to the methods of Fuhr or Cooper, but we hope to develop
suitable methods.
(values around 1--2 seem to be about right for the TREC data---see the
results section 7 below).
However, in the longer term we hope to use regression methods to
determine the constant. It is not, unfortunately, in a form directly
susceptible to the methods of Fuhr or Cooper, but we hope to develop
suitable methods.
The shape of formula 8 differs from that of formula 5
in one important respect: 8 is convex towards the upper left,
whereas 5 can under some circumstances (that is, with some
combinations of parameters) be S-shaped, increasing slowly at first,
then more rapidly, then slowly again. Averaging over a number of terms
with different values of the parameters is likely to reduce any such
effect; however, it may be useful to try a function with this
characteristic. One such, a simple combination of 8 with
a logistic function, is as follows:
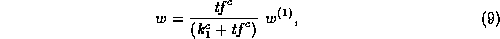
where c>1 is another unknown constant. This function has not been
tried in the present experiments.



Next: Document Length
Up: A Rough Model
Previous: The Shape of
Steve Robertson
Mon May 13 18:33:21 BST 1996
 -related weight that
has something like the characteristics (a)-(d) listed in the previous
section. Such a function can be constructed as follows. The function
-related weight that
has something like the characteristics (a)-(d) listed in the previous
section. Such a function can be constructed as follows. The function
 increases from zero to an
asymptotic maximum in approximately the right fashion. The constant
determines the rate at which the increase drops off: with a large
constant, the function is approximately linear for small
increases from zero to an
asymptotic maximum in approximately the right fashion. The constant
determines the rate at which the increase drops off: with a large
constant, the function is approximately linear for small  ,
whereas with a small constant, the effect of increasing
,
whereas with a small constant, the effect of increasing 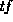 rapidly diminishes.
rapidly diminishes.



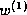 (equation
(equation 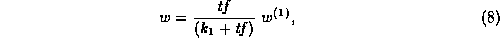
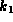 is an unknown constant.
is an unknown constant.
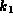 . Our approach has been to try out various values of
. Our approach has been to try out various values of 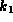 (values around 1--2 seem to be about right for the TREC data---see the
results section
(values around 1--2 seem to be about right for the TREC data---see the
results section