Description
The course revises some of the standard phase portrait methods encountered in the Dynamical Systems course in part II and extends these ideas, discussing in some detailed centres, via the use of Lyapunov functions, limit cycles and global phase portraits. The ideas of bifurcation and chaos are introduced via discrete systems.
Syllabus
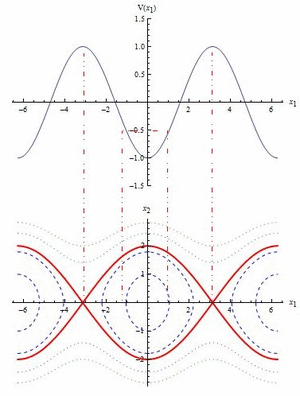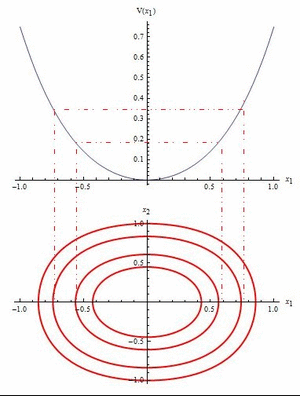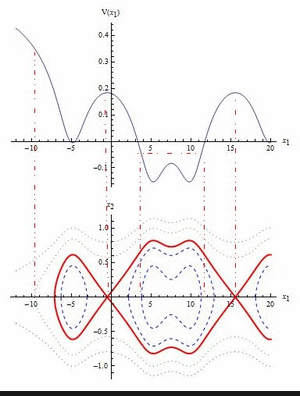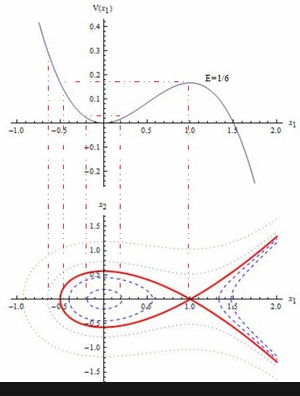
Nonlinear second order systems: Revision of linearization and classification of hyperbolic fixed points. Lyapunov functions, centres; global phase portraits; limit cycles and Poincaré -Bendixon theorem. Parameter dependent system and Hopf bifurcation.
Hamiltonian systems with first integrals: classification of fixed points, construction of global phase portraits.
Linear systems: Canonical forms and evolution operators for nth order systems.
First order discrete systems: Review of linear difference equations. The quadratic map, periodic orbits, bifurcation and chaos.
Recommended books